How does the bitcoin source code define its 21 million cap?

Many of bitcoin’s staunchest critics have expressed doubt about its 21 million cap, but perhaps the most mindless criticism relates to the fact that the supply limit is not specified in its code in plain language. That may be true, but this part of bitcoin—how exactly the supply cap is defined in its code—is relatively easy to prove.

---

---

I’ll just challenge the group to one other thing: how do you know it ends at 21 million? You all read the algorithms? You guys all believe that? I don’t know, I’ve always been a skeptic of stuff like that.

– Jamie Dimon, CEO, JP Morgan Chase, Oct 11, 2021

The bitcoin code uses a mix of consensus rules and simple math agreed upon by everyone who runs a bitcoin node to implicitly establish the limit. Here, we’ll break down the code to verify with certainty that bitcoin’s cap is 21 million. If this is a bit too technical and you’d prefer a higher-level overview of 21 million and its significance, we have that too.

The GetBlockSubsidy function

To understand what the code says about bitcoin’s total coin cap, the first place to look is the function for block subsidies. This part of the code is vital to verifying bitcoin’s fixed supply because all new bitcoin originates from block subsidies (which are included, along with transaction fees, as part of block rewards) paid to miners.

Here’s the function in bitcoin’s code that determines block subsidy, called GetBlockSubsidy():

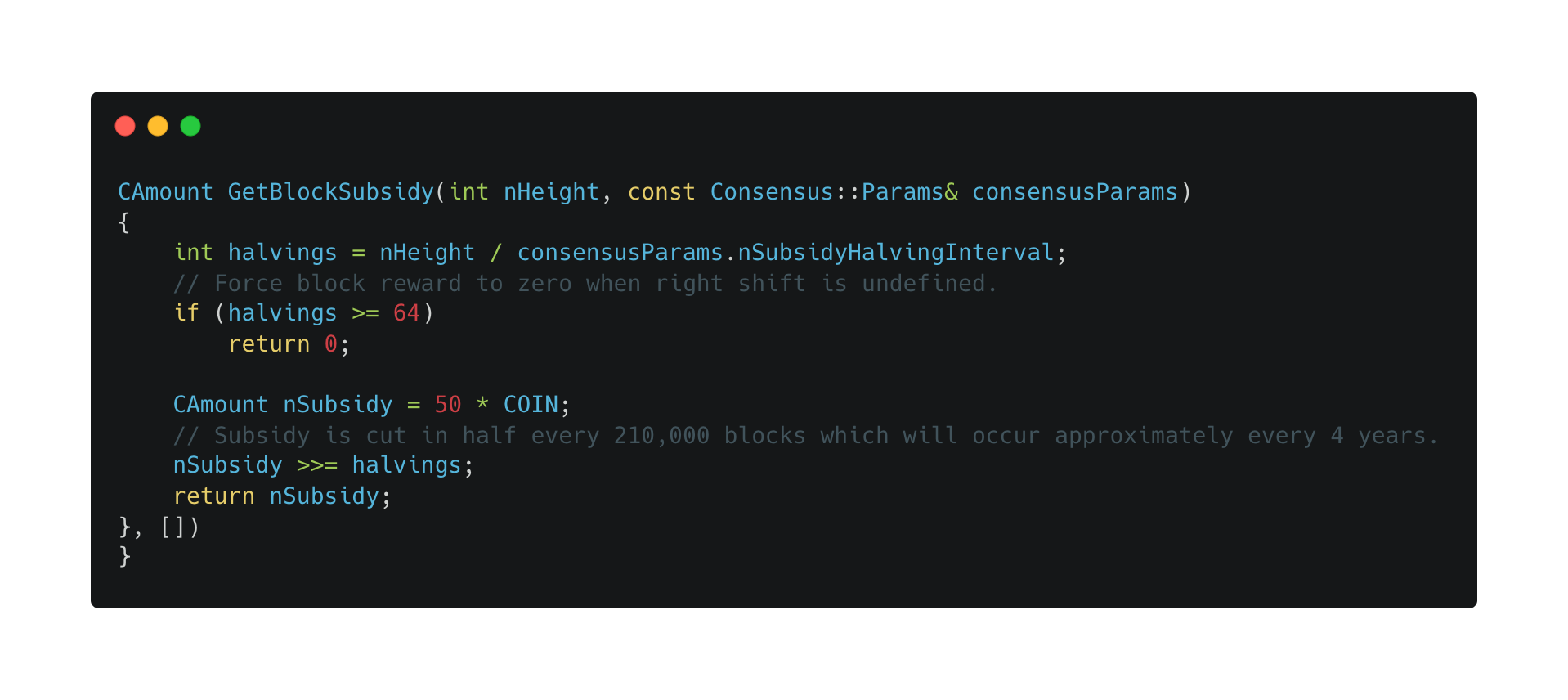
This section of code defines the amount of the block subsidy and determines the schedule for its reduction over time by way of the halvings. When the block subsidy reaches zero, it signifies bitcoin’s total supply has reached its limit. It will reach zero, eventually, due to 33 pre-programmed halvings.

Line by line, we’ll establish:

1. How the halving epoch is calculated,
2. How the block subsidy is calculated, and finally
3. How the 21 million cap is implied as a summation of the block subsidies.

1. Calculating the halving epoch

Let’s begin by looking at the way bitcoin defines how many halvings have occurred.

CAmount GetBlockSubsidy (int nHeight, const Consensus::Params& consensusParams)

This first line opens the function and specifies that what follows are the parameters for the block subsidy. Next, we get an equation that calculates the number of halvings:

int halvings = nHeight / consensusParams.nSubsidyHalvingInterval

This line says a lot, so let’s break it down:

• int halvings specifies the integer called halvings, rounded down to the nearest whole number.
• nHeight is the current number of blocks on the blockchain. When new blocks append to bitcoin’s blockchain, it grows “taller.” As of this writing, bitcoin’s “block height” is 740,805 blocks.
• nSubsidyHalvingInterval specifies the number of blocks which must pass before another halving occurs.

That last parameter, nSubsidyHalvingInterval, is a static value set to 210,000 blocks as defined elsewhere in the bitcoin codebase, shown below:

With the values for nHeight (current block height = 740,805) and nSubsidyHalvingInterval (how many blocks must pass before another halving = 210,000) in hand, we can divide the current block height by the subsidy interval. This value, which is the current halving epoch in which we find ourselves, is assigned to the integer halvings: 

int halvings = 740,805 / 210,000 or int halvings = 3.52764286 (rounds to 3)

The end result reveals we are in the epoch after the third halving. Note that before rounding down to the halving integer 3, we have the quotient 3.52764286. This number is useful, too, because it indicates we’re just beyond halfway between the third and fourth halvings.

Next, we have a comment line:

// Force block reward to zero when right shift is undefined,

This comment helps programmers and observers better understand what is happening with the code—in this case defining a bug fix to force the block reward to zero in one circumstance, as described next:

if (halvings >=64) return 0;

These lines often cause confusion because it would seem to define that there will be 64 halvings. That isn’t the case—you can read the technical details about why this bug fix was necessary if you wish.

2. Calculating the block subsidy

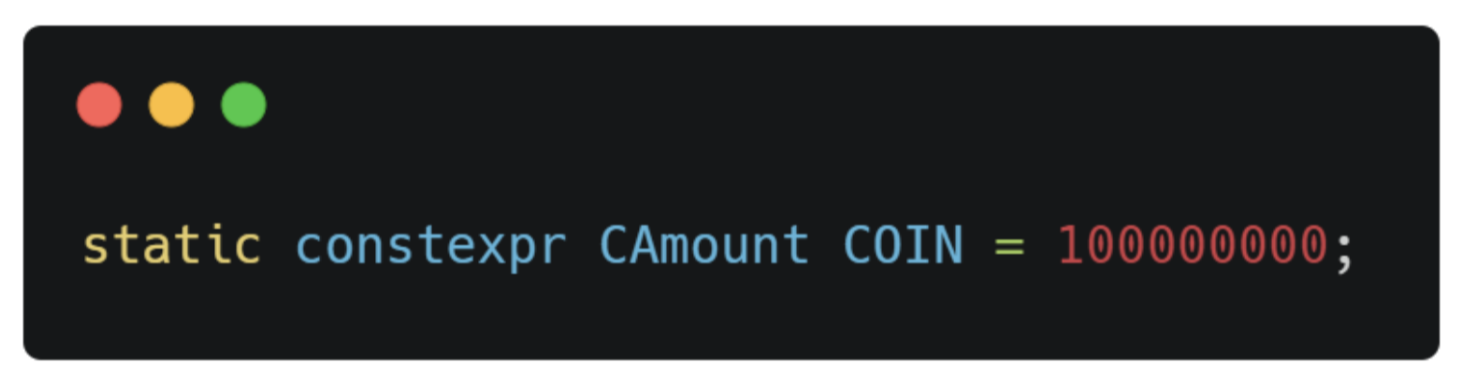
To understand how the block subsidy is calculated, you first need to know about COIN. COIN is an agreed-upon value specified elsewhere in the code as “100000000”—or the total smallest divisible units of a bitcoin. Nowadays, we call these satoshis.

Here’s the parameter in the code that specifies the amount of COIN:

CAmount nSubsidy = 50 * COIN;

The next line in the GetBlockSubsidy() function defines a fixed number equal to the block subsidy paid on each of the first set of blocks of bitcoin mined—the 210,000 blocks that occurred before the first halving. In plain English, nSubsidy is equal to 50 times the value of COIN, or 50 bitcoin.

The binary representation of nSubsidy (or 50 * 100000000) is 33 bits in length, which will be helpful later for understanding how the code divides the block subsidy with each halving:

100101010000001011111001000000000

The next line is another comment.

// Subsidy is cut in half every 210,000 blocks which will occur every 4 years.

Starting with the first block reward of “50 * COIN” (50 bitcoin), the subsidy is subsequently cut in half every 210,000 blocks. The lines below describe the function that divides the subsidy in half based on the current halving, as we first described above.

nSubsidy >>= halvings; return nSubsidy;

The critical element of the code above is the >> or “bitwise right shift”. A bitwise shift is a standard operator in the C++ programming language. Here, it means an “arithmetic shift to the right by one bit”, which is the same as dividing by two. It’s important because it helps illustrate how the supply schedule knows where to cease division.

As calculated earlier, we find ourselves today in the third halving. So, we know three things: 1) nSubsidy = 50 * 100,000,000 (or 50 bitcoin), 2) the operator >> 3;, and 3) return nSubsidy;.

The first value in our calculation above is a fixed number. The second value changes based on where we are in the halving schedule. Here again, is the binary representation for the fixed value of 50 * 100000000 (the initial block subsidy):

100101010000001011111001000000000

A single “bitwise right shift” removes the last digit on the far right from the above string. Converting these binary numbers to their decimal equivalent numbers reveals the subsidy after the first halving:

Before: 100101010000001011111001000000000 = 5,000,000,000 units of COIN (or 50 bitcoin)

After: 10010101000000101111100100000000 = 2,500,000,000 units of COIN (or 25 bitcoin)

A >>3 shifts our initial binary number by three spaces to the right, which drops the three furthest digits and creates another new number. 

Before: 100101010000001011111001000000000

After: 100101010000001011111001000000

When this new binary number is converted to its decimal equivalent, it equals 625,000,000 units of COIN, or 6.25 bitcoin.

You can visit rapidtables.com if you want to play with this operation yourself. Every time you shift by dropping an additional digit from the right side of the initial binary string, the equivalent decimal number cuts in half.

3. Summing it up

The scarcity of newly-issued bitcoin due to these bitwise right shifts, occurring every 210,000 blocks, is eye-opening:

Halving	Binary Number	Units of COIN (sats)	Bitcoin
–	100101010000001011111001000000000	5,000,000,000	50 bitcoin
1	10010101000000101111100100000000	2,500,000,000	25 bitcoin
2	1001010100000010111110010000000	1,250,000,000	12.5 bitcoin
3	100101010000001011111001000000	625,000,000	6.25 bitcoin
4	10010101000000101111100100000	312,500,000	3.125 bitcoin
5	1001010100000010111110010000	156,250,000	1.5625 bitcoin
6	100101010000001011111001000	78,125,000	78,125,000 satoshis
7	10010101000000101111100100	39,062,500	39,062,500 satoshis
8	1001010100000010111110010	19,531,250	19,531,250 satoshis
9	100101010000001011111001	9,765,625	9,765,625 satoshis
10	10010101000000101111100	4,882,812	4,882,812 satoshis
11	1001010100000010111110	2,441,406	2,441,406 satoshis
12	100101010000001011111	1,220,703	1,220,703 satoshis
13	10010101000000101111	610,351	610,351 satoshis
14	1001010100000010111	305,175	305,175 satoshis
15	100101010000001011	152,587	152,587 satoshis
16	10010101000000101	76,293	76,293 satoshis
17	1001010100000010	38,146	38,146 satoshis
18	100101010000001	19,073	19,073 satoshis
19	10010101000000	9,536	9,536 satoshis
20	1001010100000	4,768	4,768 satoshis
21	100101010000	2,384	2,384 satoshis
22	10010101000	1,192	1,192 satoshis
23	1001010100	596	596 satoshis
24	100101010	298	298 satoshis
25	10010101	149	149 satoshis
26	1001010	74	74 satoshis
27	100101	37	37 satoshis
28	10010	18	18 satoshis
29	1001	9	9 satoshis
30	100	4	4 satoshis
31	10	2	2 satoshis
32	1	1	1 satoshi

As you might have guessed, adding all the block subsidies in this table comes in just shy of 21 million, totaling 20,999,999.9769 bitcoin.

Core contributor Pieter Wuille has explained that the real total is a bit lower. While the sum of the block subsidies if collected in their entirety is 20,999,999.9769, after accounting for the coins created in the genesis block not being spendable, early bugs, and miners experimenting with the code (some blocks claimed less than allowed), the total supply is actually less—closer to 20,999,817 bitcoin.